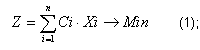«Данная статья была написана 10 лет назад. Поднятая в ней тема остаётся актуальной и по сей день, и вот, «по просьбе трудящихся», я её адаптирую под реалии сегодняшнего дня, т.е. под современное программное обеспечение (Windows 7 и Microsoft Office 2007)» — О. Виноградов
Современные руководители знают: реинжиниринг и оптимизация означают не модернизацию производства, а как раз наоборот — модернизацию самого способа ведения бизнеса. Вследствие чего, на большинстве предприятий создаются отделы маркетинга, ориентированные на изучение рынка металлов и реализацию оптимальной стратегии закупки используемых материалов. Учитывая то, что затраты на материалы в структуре себестоимости литья (в среднем) составляют 50% и абсолютная их величина значительно возрастает от года к году — снижение расходов по данной статье является одним из наиболее перспективных направлений деятельности маркетологов, менеджеров и технологов.
В данной статье на конкретном примере описана методика, позволяющая выбрать оптимальный состав компонентов шихты для производства сплавов из чёрных и цветных металлов с минимальными затратами на закупку материалов. Методика не требует специальных программ и специального обучения. Расчеты производятся с помощью стандартного пакета Excel компании Microsoft, установленного практически на каждом компьютере.
ПОДГОТОВКА ИСХОДНЫХ ДАННЫХ
Настройка Excel
Для выполнения решений описанных в статье необходимо на своём компьютере в программе Excel активизировать опцию «Поиск решения». Для этого открываем, в нашем случае, программу Excel 2007. Нажимаем на кнопку указанную красной стрелкой (Рис. 1), в выпадающем меню в правом нижнем меню выбираем указателем мышки подменю «Параметры Excel» и кликаем мышью. Открывается вкладка «Параметры Excel» (Рис. 2). Выбираем в меню «Надстройки» и в открывшемся меню «Управление надстройками» выбираем «Поиск решения» и нажимаем на кнопку «Перейти» (указана красной стрелкой).
Открывается вставка «Надстройки» (Рис. 3). Среди «Доступных надстроек» выбираем «Поиск решения» и ставим напротив неё «Птичку», нажимаем команду «ОК». Опция «Поиск решения» активизирована, о чём свидетельствует появление во вкладке «Данные» кнопки «Поиск решения» (Рис. 4).
Исходные данные
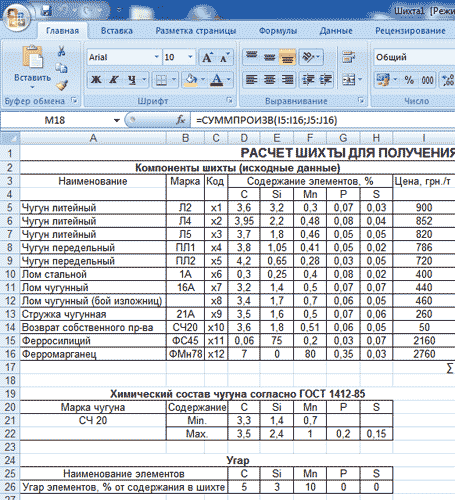
Необходимо выбрать оптимальный состав шихты для производства отливок из серого чугуна с пластинчатым графитом марки СЧ 20 по ГОСТ 1412-85 в индукционной плавильной печи ИЧТ-6,0 с кислой футеровкой. Объем завалки шихты — 6,0 т.
Выход годного литья на предприятии — 60%, угар и безвозвратные потери — 6%. Следовательно максимальный объем используемого возврата составляет — 34%
Таблица 1. Требуемый химический состав чугуна согласно ГОСТ 1412-85
| Марка | Массовая доля элементов, % | ||||
| C | Si | Mn | P | S | |
| не более | |||||
| СЧ 20 | 3,3-3,5 | 1,4-2,4 | 0,7-1,0 | 0,2 | 0,15 |
Табллица 2. Угар элементов, % от содержания в шихте (справочные данные)
| C | Si | Mn | P | S |
| 5 | 3 | 10 | — | — |
Таблица 3. Шихтовые материалы для производства чугуна предлагаемые к продаже и возврат собственного производства
| Наименование, марка | Код | Содержание контролируемых элементов, массовая доля % | Цена, грн./т | ||||
| C | Si | Mn | P | S | |||
| 1. Чугун литейный Л2 | Х1 | 3,6 | 3,2 | 0,3 | 0,07 | 0,03 | 900,00 |
| 2. Чугун литейный Л4 | Х2 | 3,95 | 2,2 | 0,48 | 0,08 | 0,04 | 852,00 |
| 3. Чугун литейный Л5 | Х3 | 3,7 | 1,8 | 0,46 | 0,05 | 0,05 | 820,00 |
| 4. Чугун передельный ПЛ1 | Х4 | 3,8 | 1,05 | 0,41 | 0,05 | 0,02 | 786,00 |
| 5. Чугун передельный ПЛ2 | Х5 | 4,2 | 0,65 | 0,28 | 0,03 | 0,05 | 720,00 |
| 6. Лом стальной 1А | Х6 | 0,3 | 0,25 | 0,4 | 0,08 | 0,02 | 400,00 |
| 7. Лом чугунный 16А | Х7 | 3,2 | 1,4 | 0,5 | 0,07 | 0,07 | 440,00 |
| 8. Лом чугунный (бой изложниц) | Х8 | 3,4 | 1,7 | 0,7 | 0,06 | 0,05 | 460,00 |
| 9. Стружка чугунная 21А | Х9 | 3,5 | 1,6 | 0,5 | 0,07 | 0,06 | 260,00 |
| 10. Возврат собственного пр-ва СЧ 20 | Х10 | 3,6 | 1,8 | 0,51 | 0,06 | 0,05 | 50,00 |
| 11. Ферросилиций ФС45 | Х11 | 0,06 | 75 | 0,2 | 0,03 | 0,07 | 2160,00 |
| 12. Ферромарганец ФМн78 | Х12 | 7,0 | — | 80 | 0,35 | 0,03 | 2760,00 |
Ввод исходных данных в таблицы Excel
Открываем Excel (в нашем случае это Excel 2007). Вносим исходные данные (Табл. №№1-3) в таблицу Excel. В результате получаем таблицу, приведенную на рис. 5. Сохраним таблицу. Для этого выбираем в меню Файл, выбираем Сохранить как, выбираем нужную папку, присваиваем имя таблице (в нашем случае Шихта1) и нажимаем Сохранить.
Предварительные расчеты
Для окончательного формирования банка исходных данных необходимо определить химический состав чугуна с учетом угара элементов. Для этого в ячейках J19; O22 построим таблицу 4.
| Табл. 4. | J | K | L | M | N | O |
| 19 | Требуемый химический состав чугуна с учетом угара, % | |||||
| 20 | Элементы | C | Si | Mn | P | S |
| 21 | Min. | C | Si | Mn | P | S |
| 22 | Max | C | Si | Mn | P | S |
Выделяем маркером ячейку К21 и вводим в нее следующее выражение =D21*0,01*(100+D26), нажи-маем Enter, т.е. минимально-допустимое содержание углерода в чугуне по ГОСТ1412-85 (ячейка D21) уве-личено на процент угара углерода (ячейка D26).
По данной схеме вводим выражения в оставшиеся ячейки таблицы:
| Адрес ячейки | Выражение |
| K22 | =D22*0,01*(100+D26) |
| L21 | =E21*0,01*(100+E26) |
| L22 | =E22*0,01*(100+E26) |
| M21 | =F21*0,01*(100+F26) |
| M22 | =F22*0,01*(100+F26) |
| N22 | =G22*0,01*(100+G26) |
| O22 | =H22*0,01*(100+H26) |
В результате мы получили таблицу (Рис. 6) в, которой в автоматическом режиме будет отражаться химический состав чугуна с учетом угара.
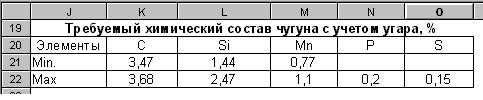
Рис. 6: Требуемый химический состав чугуна
ОПТИМИЗАЦИЯ
Теоретическая справка
В разнообразных экономических моделях планирования производства в качестве оптимального принимается план, обеспечивающий заданный производственный результат при минимальных затратах. Решением подобных задач занимается математическое программирование, наиболее изученным разделом которого является линейное программирование. В нашем случае будет использован получивший наибольшее распространение — симплекс метод, предложенный Дж. Данцигом, с помощью которого можно решить любую задачу линейного программирования.
Постановка задачи
Математически задача оптимизации состава шихты состоит в поиске минимального значения линейной функции (1):
где X1, X2, …, Xn — содержание компонентов в шихте, %;
С1, С2, …, Сn — цена компонентов шихты, грн./т.
В нашем конкретном случае функция (1) приобретает вид:
Z=900X1+852X2+820X3+786X4+720X5+400X6+440X7+460X8+260X9+50X10+2160X11+2760X12 —> Min;
при наличии линейных ограничений, заданных системой равенств и неравенств (3) — (24):
Ограничения по химическому составу:
Содержание углерода
- 3,6Х1+3,95Х2+3,7Х3+3,8Х4+4,2Х5+0,3Х6+3,2Х7+3,4Х8+3,5Х9+3,6Х10+0,06Х11+7Х12>=3,465 (3)
- 3,6Х1+3,95Х2+3,7Х3+3,8Х4+4,2Х5+0,3Х6+3,2Х7+3,4Х8+3,5Х9+3,6Х10+0,06Х11+7Х12<=3,675 (4)
где 3,465 и 3,675, соответственно, минимально и максимально допустимое содержание углерода в чугуне, с учетом угара.
Содержание кремния
- 3,2Х1+2,2Х2+1,8Х3+1,05Х4+0,65Х5+0,25Х6+1,4Х7+1,7Х8+1,6Х9+1,8Х10+75Х11>=1,442 (5)
- 3,2Х1+2,2Х2+1,8Х3+1,05Х4+0,65Х5+0,25Х6+1,4Х7+1,7Х8+1,6Х9+1,8Х10+75Х11<=2,472 (6)
где 1,442 и 2,472, соответственно, минимально и максимально допустимое содержание кремния в чугуне, с учетом угара.
Содержание марганца
- 0,3Х1+0,48Х2+0,46Х3+0,41Х4+0,28Х5+0,4Х6+0,5Х7+0,7Х8+0,5Х9+0,51Х10+0,2Х11+80Х12>=0,77 (7)
- 0,3Х1+0,48Х2+0,46Х3+0,41Х4+0,28Х5+0,4Х6+0,5Х7+0,7Х8+0,5Х9+0,51Х10+0,2Х11+80Х12<=1,10 (8)
где 0,77 и 1,10, соответственно, минимально и максимально допустимое содержание марганца в чугуне, с учетом угара.
Содержание фосфора
- 0,07Х1+0,08Х2+0,05Х3+0,05Х4+0,03Х5+0,08Х6+0,07Х7+0,06Х8+0,07Х9+0,06Х10+0,03Х11+0,35Х12<=0,2 (9)
где 0,2 — максимально допустимое содержание фосфора в чугуне, с учетом угара.
Содержание серы
- 0,03Х1+0,04Х2+0,05Х3+0,02Х4+0,05Х5+0,02Х6+0,07Х7+0,05Х8+0,06Х9+0,05Х10+0,07Х11+0,03Х12<=0,15 (10)
где 0,2 — максимально допустимое содержание серы в чугуне, с учетом угара.
Ограничения на содержание компонентов шихты:
Сумма компонентов шихты должна составлять 100% или 1 (в относительных единицах)
- Х1+Х2+Х3+Х4+Х5+Х6+Х7+Х8+Х9+Х10+Х11+Х12=1 (11)
Количество образующегося возврата у нас составляет 34%, который мы хотим использовать в полном объеме, следовательно
- Х10=0,34 (12)
Технологические ограничения на использование стружки — до 8%, следовательно
- Х9>=0 (13)
- Х9<=0,08 (14)
Считаем, что технологических ограничений по содержанию остальных компонентов шихты не существует. В этом случае необходимо учесть то, что содержание любого компонента в шихте не может принимать отрицательное значение. Для этого вводим следующие ограничения:
- Х1>=0 (15)
- Х2>=0 (16)
- Х3>=0 (17)
- Х4>=0 (18)
- Х5>=0 (19)
- Х6>=0 (20)
- Х7>=0 (21)
- Х8>=0 (22)
- Х11>=0 (23)
- Х12>=0 (24)
Таким образом, решение сформулированной задачи оптимизации сводится к решению задачи целочисленного линейного программирования, а именно к определению таких значений X1, X2, …, X12, удовлетворяющих систему ограничений (3) — (24), при которых целевая функция (2) достигает минимума.
Формирование таблиц результатов оптимизации
Продемонстрируем, как легко реализуется решение такого рода задач в среде электронных таблиц Excel.
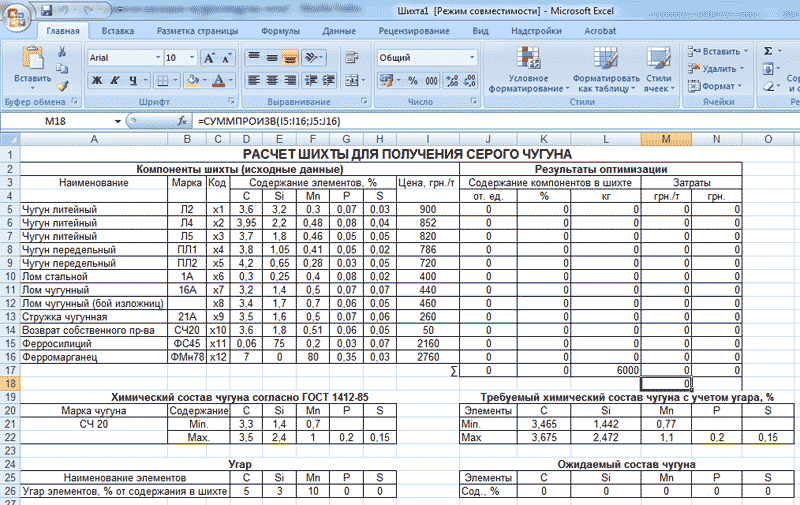
Формируем таблицы Результаты оптимизации (ячейки J2 — N17) и Ожидаемый химический состав (ячейки J24 — O26) см. Рис. 7.
В диапазон ячеек J5:J16 вводим произвольные начальные значения переменных Х1, Х2, … Х12; например, нулевое значение — 0. После проведения расчетов в данном диапазоне ячеек будет представлено требуемое содержание каждого компонента шихты в относительных единицах.
В диапазоне ячеек К5:К16 будет представлено содержание каждого компонента шихты в %. Для этого вводим расчетные формулы в каждую ячейку диапазона в соответствии с табл. 5.
Таблица 5.
| Адрес ячейки | Выражение |
| K5 | =J5*100 |
| K6 | =J6*100 |
| K7 | =J7*100 |
| K8 | =J8*100 |
| K9 | =J9*100 |
| K10 | =J10*100 |
| K11 | =J11*100 |
| K12 | =J12*100 |
| K13 | =J13*100 |
| K14 | =J14*100 |
| K15 | =J15*100 |
| K16 | =J16*100 |
В ячейку К17 введем формулу =СУММ(К5:К16), которая будет осуществлять проверку на суммарное содержание компонентов шихты — 100%.
В ячейку L17 вводим объем завалки, в кг. Мы собираемся плавить 6 т, следовательно, вводим — 6000. В диапазоне ячеек L5:L16 будет представлено необходимое содержание каждого компонента шихты в кг на объем завалки 6 т. Для выполнения расчетов введем формулы в соответствии с табл. 6.
Таблица 6.
| Адрес ячейки | Выражение |
| L5 | =J5*L17 |
| L6 | =J6*L17 |
| L7 | =J7*L17 |
| L8 | =J8*L17 |
| L9 | =J9*L17 |
| L10 | =J10*L17 |
| L11 | =J11*L17 |
| L12 | =J12*L17 |
| L13 | =J13*L17 |
| L14 | =J14*L17 |
| L15 | =J15*L17 |
| L16 | =J16*L17 |
Удельные затраты на закупку каждого компонента шихты из расчета на 1 т литья будут представлены в диапазоне ячеек М5:М16, а суммарные удельные затраты — в ячейке М17. Для их отображения введем расчетные формулы в соответствии с табл. 7
Таблица 7.
| Адрес ячейки | Выражение |
| M5 | =J5*I5 |
| M6 | =J6*I6 |
| M7 | =J7*I7 |
| M8 | =J8*I8 |
| M9 | =J9*I9 |
| M10 | =J10*I10 |
| M11 | =J11*I11 |
| M12 | =J12*I12 |
| M13 | =J13*I13 |
| M14 | =J14*I14 |
| M15 | =J15*I15 |
| M16 | =J16*I16 |
| M17 | =СУММ(М5:М16) |
Затраты на закупку каждого компонента шихты на весь объем завалки (6 тонн) определяются путем умножения цены материала на его количество (в тоннах). Затраты на закупку каждого компонента шихты в грн. будут представлены в диапазоне ячеек N5:N16, а сумма затрат на закупку всего объема шихтовых материалов в ячейке N17. Для выполнения расчетов водим формулы в соответствии с табл. 8.
Таблица 8.
| Адрес ячейки | Выражение |
| N5 | =(L5*I5)/1000 |
| N6 | =(L6*I6)/1000 |
| N7 | =(L7*I7)/1000 |
| N8 | =(L8*I8)/1000 |
| N9 | =(L9*I9)/1000 |
| N10 | =(L10*I10)/1000 |
| N11 | =(L11*I11)/1000 |
| N12 | =(L12*I12)/1000 |
| N13 | =(L13*I13)/1000 |
| N14 | =(L14*I14)/1000 |
| N15 | =(L15*I15)/1000 |
| N16 | =(L16*I16)/1000 |
| N17 | =СУММ(N5:N16) |
В ячейку J18 вносим значение целевой функции. Это значение определим с использованием встроенной математической функции СУММПРОИЗВ (1-й массив; 2-й массив). Первый массив состоит из значений цены каждого компонента шихты (диапазон ячеек I5:I16), второй массив — из значений переменных Х1, …, Х12 (диапазон ячеек J5:J16). Таким образом, в ячейку J18 необходимо ввести следующее выражение =СУММПРОИЗВ(I5:I16;J5:J16).
В ячейку К26, которая будет отражать ожидаемое содержание углерода в чугуне, вводим левые части неравенств (3) и (4). Для этого в данную ячейку вводим математическую функцию =СУММПРОИЗВ(D5:D16;$J$5:$J$16).
В ячейку L26, которая будет отражать ожидаемое содержание кремния в чугуне, вводим левые части неравенств (5) и (6). Для этого в данную ячейку вводим функцию =СУММПРОИЗВ(E5:E16;$J$5:$J$16).
В ячейку M26, которая будет отражать ожидаемое содержание марганца в чугуне, вводим левые части неравенств (7) и (8). Для этого в данную ячейку вводим функцию =СУММПРОИЗВ(F5:F16;$J$5:$J$16).
В ячейку N26, которая будет отражать ожидаемое содержание фосфора в чугуне, вводим левую часть неравенства (9). Для этого в данную ячейку вводим функцию =СУММПРОИЗВ(G5:G16;$J$5:$J$16).
В ячейку O26, которая будет отражать ожидаемое содержание серы в чугуне, вводим левую часть неравенства (10). Для этого в данную ячейку вводим функцию =СУММПРОИЗВ(Н5:Н16;$J$5:$J$16).
ПОИСК РЕШЕНИЯ
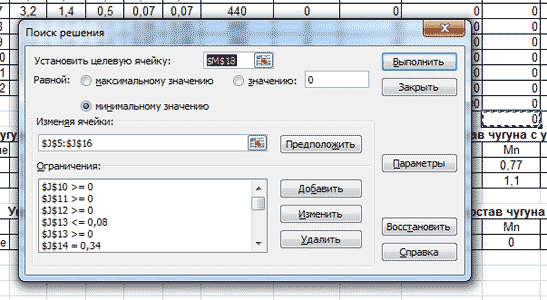
Дальнейшие действия: в меню Сервис выбираем команду Поиск решения. В появившемся диалоговом окне заполняем соответствующие поля по следующей схеме (рис. 8):
- Установить целевую ячейку — вводим адрес ячейки целевой функции (целевой ячейки). В нашем случае это ячейка М18. Следовательно в это поле вводим значение $M$18.
- Равной: максимальному значению, конкретному значению, минимальному значению. Данное поле определяет тип оптимизации (искать максмум, минимум или конкретное значение функции). Наша задача определить состав компонентов шихты с минимальной стоимостью, поэтому устанавливаем флажок в этом поле на отметке — «минимальному значению».
- Изменяя ячейки. Т.к. мы ищем минимум функции изменяя содержание компонентов шихты, которые приведены в диапазоне ячеек J5чJ16, то в данное поле вводим следующее выражение $J$5:$J$16.
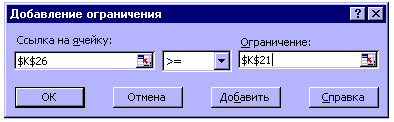
- Ограничения. В данное поле вводим линейные ограничения (3) — (24). При задании системы ограничений используется кнопка Добавить. При её нажатии появляется вспомогательное диалоговое окно, в поля которого вводятся ссылки на ячейки и ограничения, накладываемые на переменные в рассматриваемой задаче. Как видно на Рис. 8, сформированную систему ограничений в дальнейшем можно редактировать. Для этого служат кнопки Изменить и Удалить
Рассмотрим подробно каждое ограничение:
Неравенство (3) — ограничивает нижний предел содержания углерода в чугуне. Левая часть неравенства в таблице Excel отражается в ячейке К26, а правая часть неравенства в ячейке К21. Следовательно для оформления ограничения, предусмотренного неравенством (3), необходимо произвести следующие действия. В меню Поиск решения нажимаем кнопку Добавить, открывается меню Добавление ограничения (см. рис. 9), в поле Ссылка на ячейку вводим адрес ячейки, в которой производится суммирование содержания углерода в чугуне, т.е. $K$26; в поле математической операции вводим знак неравенства >=; в поле Ограничение вводим минимальнодопустимое содержание углерода в чугуне с учетом угара, значение которого рассчитано и приведено в ячейке $K$21; нажимаем кнопку Добавить, ограничение введено.
Неравенство (4) — ограничивает верхний предел содержания углерода в чугуне. Оформление огра-ничения осуществляем в той же последовательности. В меню Поиск решения нажимаем кнопку Добавить, открывается меню Добавление ограничения, в поле Ссылка на ячейку вводим адрес ячейки, в которой производится суммирование содержания углерода в чугуне, т.е. $K$26; в поле математической операции вводим знак неравенства <=; в поле Ограничение вводим максимальнодопустимое содержание углерода в чугуне с учетом угара, значение которого рассчитано и приведено в ячейке $K$22; нажимаем кнопку Добавить, ограничение введено.
Дальнейшие действия по вводу ограничений понятны, поэтому приводим только конкретные выражения, вводимые в соответствующие ячейки.
- Неравенство (5) — $L$26 >= $L$21.
- Неравенство (6) — $L$26 <= $L$22.
- Неравенство (7) — $M$26 >= $M$21.
- Неравенство (8) — $M$26 <= $M$22.
- Неравенство (9) — $N$26 <= $N$22.
- Неравенство (10) — $O$26 <= $O$22.
Равенство (11) — определяет сумму компонентов шихты, равной (в относительных единицах) 1. Суммирование компонентов шихты производится в ячейке J17, следовательно, для оформления данного ограничения мы должны ввести в соответствующие поля меню Добавление ограничения следующее выражение $J$17 = 1.
Равенство (12) — ограничивает количество используемого возврата. Содержание возврата в соста-ве шихты приведено в ячейке J14, следовательно, вводим выражение $J$14 = 0,34.
Все последующие неравенства оформляем по той же схеме.
- Неравенство (13) — $J$13 >= 0.
- Неравенство (14) — $J$13 <= 0,08.
- Неравенство (15) — $J$5 >= 0.
- Неравенство (16) — $J$6 >= 0.
- Неравенство (17) — $J$7 >= 0.
- Неравенство (18) — $J$8 >= 0.
- Неравенство (19) — $J$9 >= 0.
- Неравенство (20) — $J$10 >= 0.
- Неравенство (21) — $J$11 >= 0.
- Неравенство (22) — $J$12 >= 0.
- Неравенство (23) — $J$15 >= 0.
- Неравенство (24) — $J$16 >= 0.
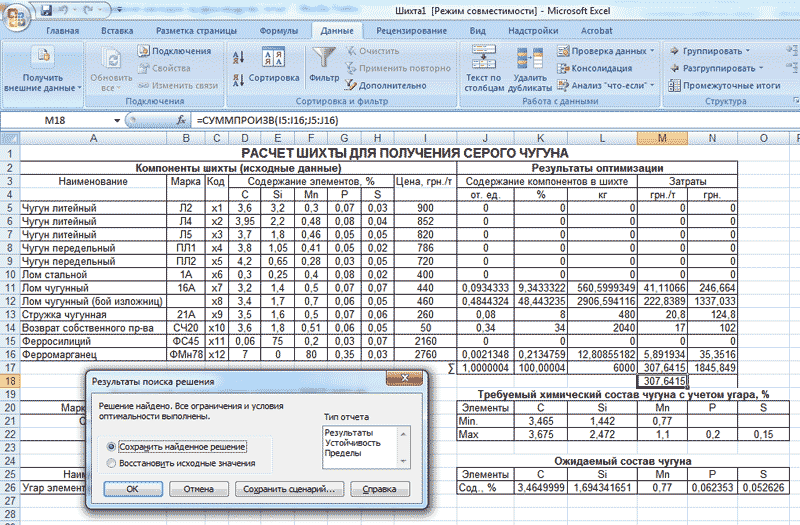
Все предусмотренные ограничения введены и теперь можно найти оптимум функции. Для этого в меню Поиск решения нажимаем на кнопку Выполнить, после чего будет осуществлена процедура Поиск решения, по результатам которой выводится сообщение о найденном решении (рис. 10).
Как видно из Рис. 10, полученные результаты можно сохранить (кнопка ОК); можно также отказаться от сохранения результатов (кнопка Отмена).
Таким образом, на рис. 6 получили искомое решение сформулированной задачи оптимизации: из имеющихся (согласно принятым условиям задачи) 16 компонентов шихты, предназначенных для получения серого чугуна марки СЧ20, программа выбрала состав шихты (в процентах и кг), обеспечивающий мини-мальную стоимость затрат на их закупку — 1845,848 грн. за 6 т шихтовых материалов или 307,6414 грн. за 1 т.
Формат сайта не позволяет расписать подробно все тонкости приводимой методики, но хочется отметить, что если произвести тот же расчет, но в условиях задачи поставить условие — максимум стоимости шихты, то получим состав завалки, стоимость которой составит — 3696,39 грн. за 6 т или 616,065 грн. за 1 т. Следовательно, из одного набора шихтовых материалов можно выплавить чугун, практически одного состава, но при этом затраты на его производство (по шихтовым материалам), могут отличаться в два раза!
ВЫВОДЫ
При разработке норм расхода шихтовых материалов и осуществлении закупок шихтовых материалов технологам и менеджерам целесообразно использовать приведенную методику оптимизации состава шихты. Для чего имеет смысл разработать программу в с++, позволяющую формировать симплекс таблицы исходя из количества требуемых элементов в составе сплава и количества компонентов шихты. Это особенно актуально при производстве многокомпонентных сплавов и при больших потоках производства, экономия может быть очень значительна.
Описанная методика построена на использовании электронных таблиц Excel, обладающих мощным встроенным математическим аппаратом, что обеспечивает поиск решения при использовании любого количества компонентов шихты и проведении расчетов на практически любое количество элементов, получаемого сплава.